Linear Regression Plot with Seaborn, 통계를 위한 statsmodels 라이브러리

Seaborn

Python에서 많이 쓰이는 시각화 라이브러리. http://seaborn.pydata.org

%matplotlib inline
import pandas as pd
import seaborn as sb
import matplotlib as plt

cars = pd.read_csv('automobile.csv')
cars.head()

	symboling	maker	fuel	aspiration	doors	body	wheels	engine_location	wheel_base	...
0	2	audi	gas	std	four	sedan	fwd	front	99.8	...
1	2	audi	gas	std	four	sedan	4wd	front	99.4	...
2	1	audi	gas	std	four	sedan	fwd	front	105.8	...
3	1	audi	gas	turbo	four	sedan	fwd	front	105.8	...
4	2	bmw	gas	std	two	sedan	rwd	front	101.2	...

5 rows × 26 columns

cars.columns

Index(['symboling', 'normalized_losses', 'maker', 'fuel', 'aspiration',
       'doors', 'body', 'wheels', 'engine_location', 'wheel_base', 'length',
       'width', 'height', 'curb_weight', 'engine_type', 'cylinders',
       'engine_size', 'fuel_system', 'bore', 'stroke', 'compression_ratio',
       'horsepower', 'peak_rpm', 'city_mpg', 'highway_mpg', 'price'],
      dtype='object')

Regression Plot

# 노트북에 표시되는 plot 크기 조절

fig = plt.pyplot.gcf()
fig.set_size_inches(16, 10)

<matplotlib.figure.Figure at 0x28d98908898>

sb.regplot(cars.length, cars.symboling)

<matplotlib.axes._subplots.AxesSubplot at 0x28d989199b0>

png

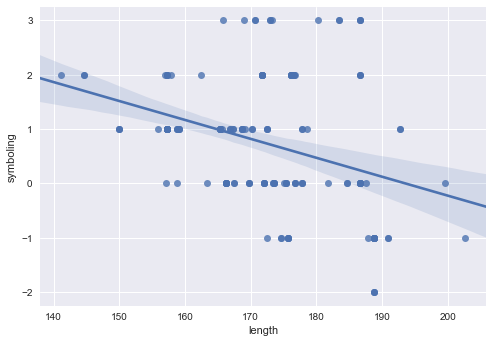
sb.regplot('length', 'symboling', data=cars)

<matplotlib.axes._subplots.AxesSubplot at 0x28d989d5630>

png

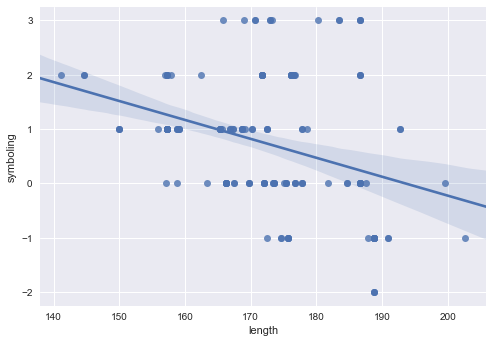
# 회귀선 지우기

sb.regplot('length', 'symboling', data=cars, fit_reg=False)

<matplotlib.axes._subplots.AxesSubplot at 0x28d98a33b38>

png

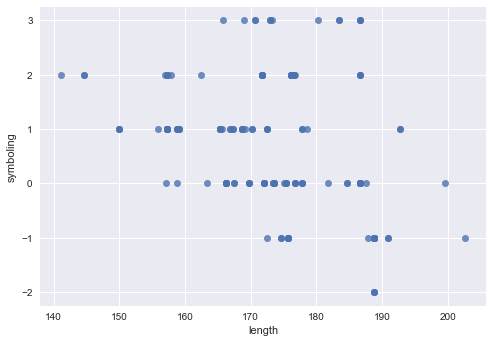
# jitter

sb.regplot('length', 'symboling', data=cars, y_jitter=0.1)

<matplotlib.axes._subplots.AxesSubplot at 0x28d98be3be0>

png

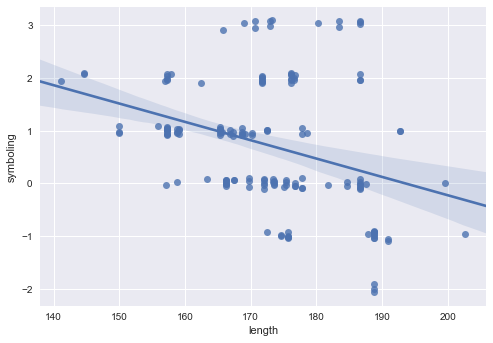
# 신뢰구간(ci) 지우기. 회귀선 색상. 점 색상.

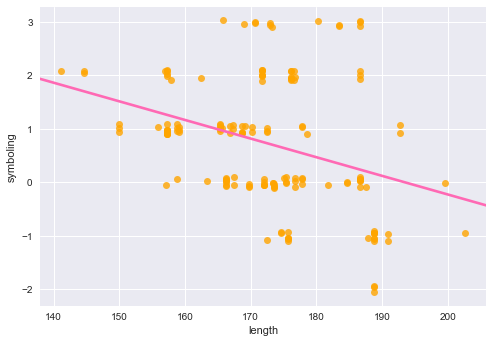
sb.regplot('length', 'symboling', data=cars, y_jitter=0.1, ci=None, 
           line_kws={'color': 'hotpink'}, 
           scatter_kws={'color': 'orange'})   # 16진수('FF9900')로 색상 지정 가능.

<matplotlib.axes._subplots.AxesSubplot at 0x28d98c24320>

png

# 점 모양과 크기

http://matplotlib.org/api/markers_api.html#module-matplotlib.markers

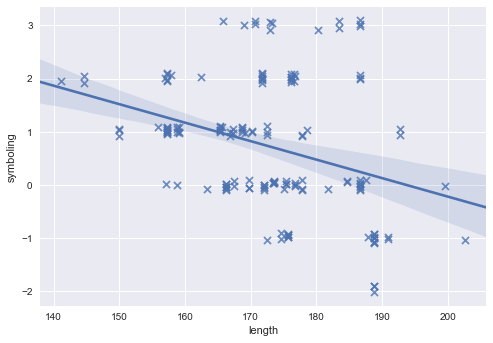
sb.regplot('length', 'symboling', data=cars, y_jitter=0.1, marker='x', scatter_kws={'s': 50})

<matplotlib.axes._subplots.AxesSubplot at 0x28d98c8ce48>

png

# save plot

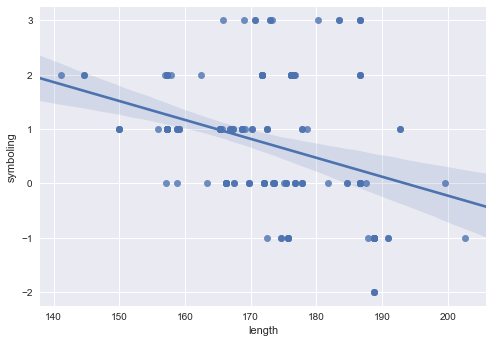
plot = sb.regplot('length', 'symboling', data=cars)
plot.get_figure().savefig('plot.png')

png

statsmodels

Python에서 통계 분석을 위한 라이브러리. http://statsmodels.sourceforge.net/

import statsmodels.formula.api as smf

model = smf.ols('symboling ~ length', data=cars)
result = model.fit()
result.summary()

OLS Regression Results
Dep. Variable:	symboling	R-squared:	0.113
Model:	OLS	Adj. R-squared:	0.107
Method:	Least Squares	F-statistic:	20.01
Date:	Sat, 25 Mar 2017	Prob (F-statistic):	1.47e-05
Time:	10:47:16	Log-Likelihood:	-243.64
No. Observations:	159	AIC:	491.3
Df Residuals:	157	BIC:	497.4
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[95.0% Conf. Int.]
Intercept	6.7385	1.345	5.011	0.000	4.082 9.395
length	-0.0348	0.008	-4.474	0.000	-0.050 -0.019

Omnibus:	10.632	Durbin-Watson:	0.909
Prob(Omnibus):	0.005	Jarque-Bera (JB):	11.510
Skew:	0.658	Prob(JB):	0.00317
Kurtosis:	2.915	Cond. No.	2.60e+03

model = smf.ols('symboling ~ length + price', data=cars).fit().summary()

# smf.ols('symboling ~ .', data=cont_data).fit().summary()   # ~ 다음에 '.' 인식 안됨

연속형 / 범주형 변수 구분

cars.columns

Index(['symboling', 'normalized_losses', 'maker', 'fuel', 'aspiration',
       'doors', 'body', 'wheels', 'engine_location', 'wheel_base', 'length',
       'width', 'height', 'curb_weight', 'engine_type', 'cylinders',
       'engine_size', 'fuel_system', 'bore', 'stroke', 'compression_ratio',
       'horsepower', 'peak_rpm', 'city_mpg', 'highway_mpg', 'price'],
      dtype='object')

cont_var = cars.columns[cars.dtypes != 'object']
cont_var

Index(['symboling', 'normalized_losses', 'wheel_base', 'length', 'width',
       'height', 'curb_weight', 'engine_size', 'bore', 'stroke',
       'compression_ratio', 'horsepower', 'peak_rpm', 'city_mpg',
       'highway_mpg', 'price'],
      dtype='object')

cate_var = cars.columns[cars.dtypes == 'object']
cate_var

Index(['maker', 'fuel', 'aspiration', 'doors', 'body', 'wheels',
       'engine_location', 'engine_type', 'cylinders', 'fuel_system'],
      dtype='object')

cars[cate_var].head()

	maker	fuel	aspiration	doors	body	wheels	engine_location	engine_type	cylinders	fuel_system
0	audi	gas	std	four	sedan	fwd	front	ohc	four	mpfi
1	audi	gas	std	four	sedan	4wd	front	ohc	five	mpfi
2	audi	gas	std	four	sedan	fwd	front	ohc	five	mpfi
3	audi	gas	turbo	four	sedan	fwd	front	ohc	five	mpfi
4	bmw	gas	std	two	sedan	rwd	front	ohc	four	mpfi

연속형 변수들만 사용 (범주형 변수 제외)

indep = ' + '.join(cont_var.difference(['symboling']))   # symboling 제외
indep

'bore + city_mpg + compression_ratio + curb_weight + engine_size + height + highway_mpg + horsepower + length + normalized_losses + peak_rpm + price + stroke + wheel_base + width'

smf.ols('symboling ~ ' + indep, data=cars).fit().summary()

OLS Regression Results
Dep. Variable:	symboling	R-squared:	0.593
Model:	OLS	Adj. R-squared:	0.550
Method:	Least Squares	F-statistic:	13.89
Date:	Sat, 25 Mar 2017	Prob (F-statistic):	3.68e-21
Time:	10:47:16	Log-Likelihood:	-181.72
No. Observations:	159	AIC:	395.4
Df Residuals:	143	BIC:	444.5
Df Model:	15
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[95.0% Conf. Int.]
Intercept	3.3079	5.583	0.592	0.554	-7.728 14.344
bore	-0.1778	0.368	-0.484	0.629	-0.905 0.549
city_mpg	-0.1086	0.052	-2.072	0.040	-0.212 -0.005
compression_ratio	0.0456	0.026	1.741	0.084	-0.006 0.097
curb_weight	-0.0007	0.001	-1.179	0.241	-0.002 0.000
engine_size	0.0030	0.006	0.471	0.638	-0.010 0.016
height	0.0492	0.046	1.068	0.287	-0.042 0.140
highway_mpg	0.0847	0.047	1.800	0.074	-0.008 0.178
horsepower	0.0054	0.006	0.966	0.336	-0.006 0.017
length	0.0050	0.016	0.310	0.757	-0.027 0.037
normalized_losses	0.0140	0.002	6.236	0.000	0.010 0.018
peak_rpm	-0.0001	0.000	-0.757	0.450	-0.001 0.000
price	8.963e-06	2.8e-05	0.320	0.750	-4.64e-05 6.44e-05
stroke	-0.0668	0.268	-0.249	0.803	-0.597 0.463
wheel_base	-0.2074	0.031	-6.669	0.000	-0.269 -0.146
width	0.2207	0.081	2.716	0.007	0.060 0.381

Omnibus:	0.983	Durbin-Watson:	1.035
Prob(Omnibus):	0.612	Jarque-Bera (JB):	0.833
Skew:	0.177	Prob(JB):	0.659
Kurtosis:	3.013	Cond. No.	1.22e+06

Python Linear Model