Data Mining - Neural Network
# 홈쇼핑에서 반품 고객의 특성을 파악하고자 인공신경망 분석 활용
인공신경망 이론 (링크)
1. Neural Network Analysis using "nnet" package
library(nnet)
library(caret)
library(ROCR)
cb <- read.delim("data/Hshopping.txt", stringsAsFactors=FALSE)
head(cb)
## ID 성별 나이 구매금액 출연자 반품여부
## 1 1 1 33 2 2 0
## 2 2 2 21 3 2 1
## 3 3 1 45 1 1 0
## 4 4 1 50 2 1 0
## 5 5 1 21 3 1 1
## 6 6 1 22 3 1 1
summary(cb$반품여부)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 0.000 0.000 0.312 1.000 1.000
cb$반품여부 <- factor(cb$반품여부) # 명목형 값 예측일 경우 factor로 변환.
summary(cb$반품여부)
## 0 1
## 344 156
# 데이터 분할
set.seed(1)
inTrain <- createDataPartition(y=cb$반품여부, p=0.6, list=FALSE)
cb.train <- cb[inTrain,]
cb.test <- cb[-inTrain,]
# 모델링
# nnet의 주요 옵션들
# size : hidden node 수
# maxit : 반복횟수
# decay : overfitting을 피하기 위해 사용하는 weight decay parameter
# rang : Initial random weights on [-rang, rang]. default 0.5
set.seed(123)
nn_model1 <- nnet(반품여부 ~ 성별+나이+구매금액+출연자, data=cb.train, size=3, maxit=1000)
## # weights: 19
## initial value 200.606812
## iter 10 value 86.410893
## iter 20 value 81.774551
## iter 30 value 76.044092
## iter 40 value 66.203022
## iter 50 value 63.924238
## iter 60 value 63.114128
## iter 70 value 62.903511
.........
## iter 400 value 49.402414
## iter 410 value 49.402301
## iter 420 value 49.401785
## iter 430 value 49.401572
## iter 440 value 49.401474
## iter 450 value 49.401280
## iter 460 value 49.400976
## final value 49.400929
## converged
nn_model2 <- nnet(반품여부 ~ 성별+나이+구매금액+출연자, data=cb.train, size=5, maxit=1000, decay = 0.0005, rang = 0.1)
## # weights: 31
## initial value 197.970465
## iter 10 value 75.903511
## iter 20 value 64.938108
## iter 30 value 60.738498
## iter 40 value 57.431605
## iter 50 value 55.116059
## iter 60 value 52.363732
## iter 70 value 51.978971
.........
## iter 400 value 41.291765
## iter 410 value 41.277988
## iter 420 value 41.253266
## iter 430 value 41.245844
## iter 440 value 41.244417
## iter 450 value 41.243771
## final value 41.243740
## converged
summary(nn_model1)
## a 4-3-1 network with 19 weights
## options were - entropy fitting
## b->h1 i1->h1 i2->h1 i3->h1 i4->h1
## 26.33 -101.85 3.32 -69.49 47.08
## b->h2 i1->h2 i2->h2 i3->h2 i4->h2
## -243.83 100.35 -7.51 97.79 20.53
## b->h3 i1->h3 i2->h3 i3->h3 i4->h3
## -86.52 -17.34 5.66 18.53 -74.97
## b->o h1->o h2->o h3->o
## 0.57 -35.69 53.31 -2.57
summary(nn_model2)
## a 4-5-1 network with 31 weights
## options were - entropy fitting decay=5e-04
## b->h1 i1->h1 i2->h1 i3->h1 i4->h1
## 17.56 -11.75 1.73 2.07 -30.40
## b->h2 i1->h2 i2->h2 i3->h2 i4->h2
## 38.28 -18.18 0.89 -14.03 3.08
## b->h3 i1->h3 i2->h3 i3->h3 i4->h3
## 15.28 -30.77 0.63 -14.48 16.85
## b->h4 i1->h4 i2->h4 i3->h4 i4->h4
## 6.20 -15.06 0.42 -9.73 7.21
## b->h5 i1->h5 i2->h5 i3->h5 i4->h5
## 2.56 20.42 -1.17 6.20 4.74
## b->o h1->o h2->o h3->o h4->o h5->o
## 5.48 -3.03 -13.77 21.03 -28.93 9.62
library(devtools)
source_url('https://gist.githubusercontent.com/Peque/41a9e20d6687f2f3108d/raw/85e14f3a292e126f1454864427e3a189c2fe33f3/nnet_plot_update.r')
plot.nnet(nn_model1)

plot.nnet(nn_model2)

# 위 인공신경망 모델에서 각 변수의 중요도 확인
library(NeuralNetTools)
garson(nn_model1)

garson(nn_model2)

# 두 모델의 테스트 데이터셋에 대한 예측력/성능 비교
# nn_model1
confusionMatrix(predict(nn_model1, newdata=cb.test, type="class"), cb.test$반품여부)
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 121 12
## 1 16 50
##
## Accuracy : 0.8593
## 95% CI : (0.8031, 0.9044)
## No Information Rate : 0.6884
## P-Value [Acc > NIR] : 1.999e-08
##
## Kappa : 0.6777
## Mcnemar's Test P-Value : 0.5708
##
## Sensitivity : 0.8832
## Specificity : 0.8065
## Pos Pred Value : 0.9098
## Neg Pred Value : 0.7576
## Prevalence : 0.6884
## Detection Rate : 0.6080
## Detection Prevalence : 0.6683
## Balanced Accuracy : 0.8448
##
## 'Positive' Class : 0
##
# nn_model2
confusionMatrix(predict(nn_model2, newdata=cb.test, type="class"), cb.test$반품여부)
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 126 11
## 1 11 51
##
## Accuracy : 0.8894
## 95% CI : (0.8374, 0.9294)
## No Information Rate : 0.6884
## P-Value [Acc > NIR] : 1.98e-11
##
## Kappa : 0.7423
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.9197
## Specificity : 0.8226
## Pos Pred Value : 0.9197
## Neg Pred Value : 0.8226
## Prevalence : 0.6884
## Detection Rate : 0.6332
## Detection Prevalence : 0.6884
## Balanced Accuracy : 0.8711
##
## 'Positive' Class : 0
##
# ROCR::prediction - ROCR 패키지에 있는 prediction 함수 사용.
# model1
nn_pred1 <- ROCR::prediction(predict(nn_model1, newdata=cb.test, type="raw"), cb.test$반품여부)
nn_model1.roc <- performance(nn_pred1, "tpr", "fpr") # ROC-chart
plot(nn_model1.roc, colorize=TRUE)

nn_model1.lift <- performance(nn_pred1, "lift", "rpp") # Lift chart
plot(nn_model1.lift, colorize=TRUE)

# model2
nn_pred2 <- ROCR::prediction(predict(nn_model2, newdata=cb.test, type="raw"), cb.test$반품여부)
nn_model2.roc <- performance(nn_pred2, "tpr", "fpr") # ROC-chart
plot(nn_model2.roc, colorize=TRUE)

nn_model2.lift <- performance(nn_pred2, "lift", "rpp") # Lift chart
plot(nn_model2.lift, colorize=TRUE)

2. Neural Network Analysis using "neuralnet" package
library(neuralnet)
cb <- read.delim("data/Hshopping.txt", stringsAsFactors=FALSE) # neuralnet 패키지는 목표변수가 numeric.
# 데이터 분할
set.seed(1)
inTrain <- createDataPartition(y=cb$반품여부, p=0.6, list=FALSE)
cb.train <- cb[inTrain,]
cb.test <- cb[-inTrain,]
# 모델링
set.seed(123)
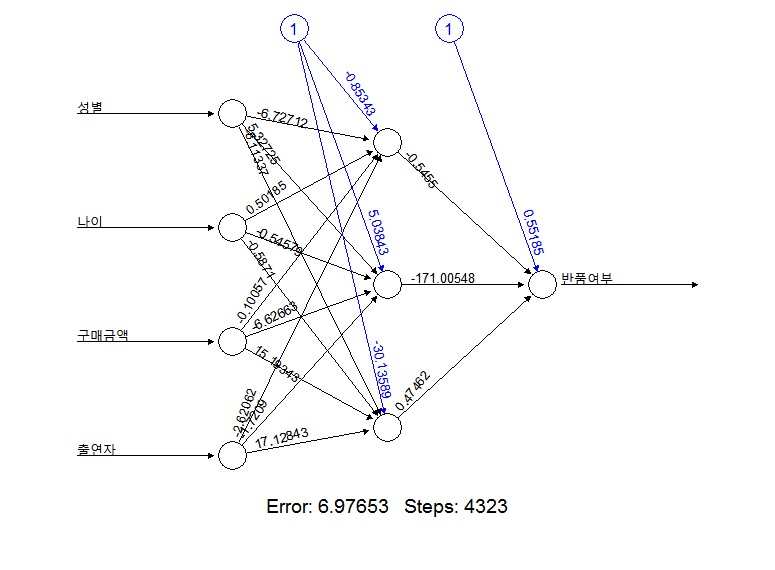
nnet_model1 <- neuralnet(반품여부 ~ 성별+나이+구매금액+출연자, data=cb.train, hidden=3, threshold=0.01)
nnet_model2 <- neuralnet(반품여부 ~ 성별+나이+구매금액+출연자, data=cb.train, hidden=c(2,2), threshold=0.01)
# threshold : 에러의 감소분이 threshold 값보다 작으면 stop
# hidden : hidden node 수.
# hidden=c(2,2) : hidden layer 2개가 각각 hidden node 2개를 가짐
# linear.output: 활성함수('logistic' or 'tanh')가 출력 뉴런에 적용되지 않아야 하는 경우(즉, 회귀) TRUE로 설정(default)
# stepmax: 훈련 수행 최대 횟수
plot(nnet_model1)
plot(nnet_model2)
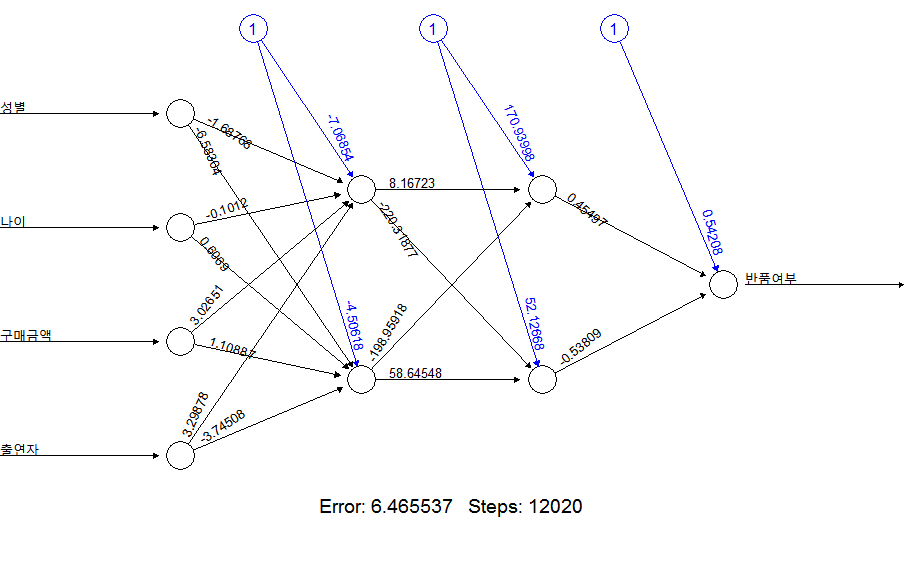
# 모델 내에서 각 변수의 영향도(일반화 가중치)
# 나이 : 분산이 0에 가까움. 결과에 미치는 영향이 미미하다.
par(mfrow=c(2,2))
gwplot(nnet_model1, selected.covariate = "성별", min=-3,max=6)
gwplot(nnet_model1, selected.covariate = "나이", min=-3,max=6)
gwplot(nnet_model1, selected.covariate = "구매금액", min=-3,max=6)
gwplot(nnet_model1, selected.covariate = "출연자", min=-3,max=6)

par(mfrow=c(1,1))
# 테스트 데이터에서 필요한 필드만 지정!!!
# nnet_model1
cb.test$nnet1_pred_prob <- compute(nnet_model1, covariate=cb.test[, c(2:5)])$net.result
cb.test$nnet1_pred <- ifelse(cb.test$nnet1_pred_prob > 0.5, 1, 0)
confusionMatrix(cb.test$nnet1_pred, cb.test$반품여부)
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 128 13
## 1 13 46
##
## Accuracy : 0.87
## 95% CI : (0.8153477, 0.9132916)
## No Information Rate : 0.705
## P-Value [Acc > NIR] : 0.00000002942981
##
## Kappa : 0.6874624
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.9078014
## Specificity : 0.7796610
## Pos Pred Value : 0.9078014
## Neg Pred Value : 0.7796610
## Prevalence : 0.7050000
## Detection Rate : 0.6400000
## Detection Prevalence : 0.7050000
## Balanced Accuracy : 0.8437312
##
## 'Positive' Class : 0
##
# nnet_model2
cb.test$nnet2_pred_prob <- compute(nnet_model2, covariate=cb.test[, c(2:5)])$net.result
cb.test$nnet2_pred <- ifelse(cb.test$nnet2_pred_prob > 0.5, 1, 0)
confusionMatrix(cb.test$nnet2_pred, cb.test$반품여부)
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 128 17
## 1 13 42
##
## Accuracy : 0.85
## 95% CI : (0.7928413, 0.8964505)
## No Information Rate : 0.705
## P-Value [Acc > NIR] : 0.000001340647
##
## Kappa : 0.6321275
## Mcnemar's Test P-Value : 0.5838824
##
## Sensitivity : 0.9078014
## Specificity : 0.7118644
## Pos Pred Value : 0.8827586
## Neg Pred Value : 0.7636364
## Prevalence : 0.7050000
## Detection Rate : 0.6400000
## Detection Prevalence : 0.7250000
## Balanced Accuracy : 0.8098329
##
## 'Positive' Class : 0
##
# ROC & Lift chart
nnet1_pred <- ROCR::prediction(cb.test$nnet1_pred_prob, cb.test$반품여부)
nnet_model1.roc <- performance(nnet1_pred, "tpr", "fpr") # ROC-chart
plot(nnet_model1.roc, colorize=TRUE)

nnet_model1.lift <- performance(nnet1_pred, "lift", "rpp") # Lift chart
plot(nnet_model1.lift, colorize=TRUE)

nnet2_pred <- ROCR::prediction(cb.test$nnet2_pred_prob, cb.test$반품여부)
nnet_model2.roc <- performance(nnet2_pred, "tpr", "fpr") # ROC-chart
##### Input Normalization in Neural Networks
# 입력값 정규화
# 값을 0 ~ 1 사이의 값으로 변환
normalize <- function (x) {
normalized = (x - min(x)) / (max(x) - min(x))
return(normalized)
}
cb <- read.delim("data/Hshopping.txt", stringsAsFactors=FALSE)
# 나이와 구매금액을 정규화
cb$나이 <- normalize(cb$나이)
cb$구매금액 <- normalize(cb$구매금액)
head(cb)
## ID 성별 나이 구매금액 출연자 반품여부
## 1 1 1 0.2666666667 0.5 2 0
## 2 2 2 0.1066666667 1.0 2 1
## 3 3 1 0.4266666667 0.0 1 0
## 4 4 1 0.4933333333 0.5 1 0
## 5 5 1 0.1066666667 1.0 1 1
## 6 6 1 0.1200000000 1.0 1 1
set.seed(1)
inTrain <- createDataPartition(y=cb$반품여부, p=0.6, list=FALSE)
cb.train <- cb[inTrain,]
cb.test <- cb[-inTrain,]
set.seed(123)
nnet_model3 <- neuralnet(반품여부 ~ 성별+나이+구매금액+출연자, data=cb.train, hidden=3, threshold=0.01)
par(mfrow=c(2,2))
gwplot(nnet_model3, selected.covariate = "성별", min=-3, max=6)
gwplot(nnet_model3, selected.covariate = "나이", min=-3, max=6)
gwplot(nnet_model3, selected.covariate = "구매금액", min=-3, max=6)
gwplot(nnet_model3, selected.covariate = "출연자", min=-3, max=6)

par(mfrow=c(1,1))
garson(nnet_model3)

cb.test$nnet3_pred_prob <- compute(nnet_model3, covariate=cb.test[, c(2:5)])$net.result
cb.test$nnet3_pred <- ifelse(cb.test$nnet3_pred_prob > 0.5, 1, 0)
confusionMatrix(cb.test$nnet3_pred, cb.test$반품여부)
## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 131 12
## 1 10 47
##
## Accuracy : 0.89
## 95% CI : (0.8382038, 0.9297668)
## No Information Rate : 0.705
## P-Value [Acc > NIR] : 0.0000000003254392
##
## Kappa : 0.7329125
## Mcnemar's Test P-Value : 0.8311704
##
## Sensitivity : 0.9290780
## Specificity : 0.7966102
## Pos Pred Value : 0.9160839
## Neg Pred Value : 0.8245614
## Prevalence : 0.7050000
## Detection Rate : 0.6550000
## Detection Prevalence : 0.7150000
## Balanced Accuracy : 0.8628441
##
## 'Positive' Class : 0
##
# Model Comparison
nnet3_pred <- ROCR::prediction(cb.test$nnet3_pred_prob, cb.test$반품여부)
nnet_model3.roc <- performance(nnet3_pred, "tpr", "fpr") # ROC-chart
plot(nnet_model1.roc, col="red")
plot(nnet_model2.roc, col="green", add=T)
plot(nnet_model3.roc, col="blue", add=T)
legend(0.6,0.7,c("nnet_model1","nnet_model2","nnet_model3"),cex=0.9,col=c("red","green","blue"),lty=1)

performance(nnet1_pred, "auc")@y.values[[1]]
## [1] 0.8942781584
performance(nnet2_pred, "auc")@y.values[[1]]
## [1] 0.9343070081
performance(nnet3_pred, "auc")@y.values[[1]]
## [1] 0.9308210121
3. "Multinomial Classification" using neuralnet
# iris 데이터 다항 분류
data(iris)
summary(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300000 Min. :2.000000 Min. :1.000 Min. :0.100000
## 1st Qu.:5.100000 1st Qu.:2.800000 1st Qu.:1.600 1st Qu.:0.300000
## Median :5.800000 Median :3.000000 Median :4.350 Median :1.300000
## Mean :5.843333 Mean :3.057333 Mean :3.758 Mean :1.199333
## 3rd Qu.:6.400000 3rd Qu.:3.300000 3rd Qu.:5.100 3rd Qu.:1.800000
## Max. :7.900000 Max. :4.400000 Max. :6.900 Max. :2.500000
## Species
## setosa :50
## versicolor:50
## virginica :50
# neuralnet은 식에서 '.'을 지원하지 않기 때문에 아래와 같이 식을 문자열로 생성.
formula <- as.formula(paste('Species ~ ', paste(names(iris)[-length(iris)], collapse='+')))
formula
## Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
# neuralnet does not support the '.' notation in the formula.
# multi_model <- neuralnet(formula, iris, hidden=3, linear.output=FALSE)
# fails !
# Species가 factor : neuralnet 패키지는 target으로 factor를 사용할 수 없다.
# Species를 3개의 binary 변수로 펼쳐야 한다.
formula <- as.formula(paste('setosa + versicolor + virginica ~ ', paste(names(iris)[-length(iris)], collapse='+')))
formula
## setosa + versicolor + virginica ~ Sepal.Length + Sepal.Width +
## Petal.Length + Petal.Width
trainData <- cbind(iris[, 1:4], class.ind(iris$Species))
head(trainData)
## Sepal.Length Sepal.Width Petal.Length Petal.Width setosa versicolor
## 1 5.1 3.5 1.4 0.2 1 0
## 2 4.9 3.0 1.4 0.2 1 0
## 3 4.7 3.2 1.3 0.2 1 0
## 4 4.6 3.1 1.5 0.2 1 0
## 5 5.0 3.6 1.4 0.2 1 0
## 6 5.4 3.9 1.7 0.4 1 0
## virginica
## 1 0
## 2 0
## 3 0
## 4 0
## 5 0
## 6 0
multi_model <- neuralnet(formula, trainData, hidden=3)
plot(multi_model)
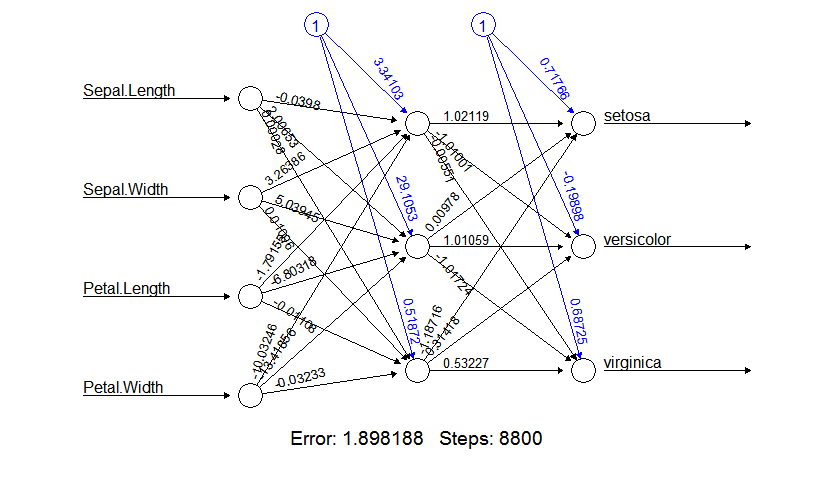
species_prob = compute(multi_model, iris[, 1:4])$net.result
head(species_prob)
## [,1] [,2] [,3]
## [1,] 0.9999999967 -0.00066075253881 0.00063389434950
## [2,] 0.9999999929 0.00101469292227 -0.00100920304022
## [3,] 0.9999999945 0.00030837464151 -0.00031652175015
## [4,] 0.9999999920 0.00141887532902 -0.00140558183794
## [5,] 0.9999999970 -0.00080825597291 0.00077854991315
## [6,] 0.9999999954 -0.00009871907406 0.00008271214732


